Este post es sobre una algoritmo que es la madre del cordero de muchos algoritmos de búsqueda ? Se puede considerar un algoritmo base para búsquedas, sobre el que se puede evolucionar hacia otros algoritmos. No he encontrado su implementación en PHP, así que aquí estoy compartiendo, a modo de codekata, este howto.
Este algoritmo general de búsqueda en grafos, es un algoritmo elaborado para solucionar problemas inteligentemente representados mediante grafos. No aplica ninguna predicción sobre los siguientes caminos a seguir mientras se hace la búsqueda, pero tampoco es un algoritmo de fuerza bruta.
Lo propuso Nilsson en 1971, así que tiene ya su recorrido. A partir de éste se han generado todo tipo de mejoras, heurísticas, desembocando en todo tipo de variantes que mejorarán el rendimiento como por ejemplo el A*, IDA, SMA*, Dijkstra, etcétera..
Porqué los grafos, dónde se usan
Los grafos pueden representar muchas cosas, como por ejemplo el recorrido de laberintos, la navegación por mapas, la búsqueda de soluciones a juegos de tablero, el cómo generar comportamientos inteligentes en videojuegos, robots que se mueven por escenarios conocidos o desconocidos, búsqueda de soluciones a problemas que implican desgranar árboles (que son un tipo de grafos), etcétera..
Hay muchas variantes según los nodos o los arcos. Pueden ser dirigidos o no, según sus arcos tengan dirección o no. También dichos arcos pueden tener pesos o costes, los nodos también. Además de que en cada nodo podemos tener toda la información que se necesite.
Con todo esto junto, y atendiendo a los algoritmos para resolver los problemas, tendremos sus variantes.
Cómo representar escenarios en grafos
Como caso general, este codekata plantea un escenario simple, en el que hay que ir de un punto A a un punto B. Lo siguiente para comprender el funcionamiento, es comprender cómo representar un escenario en un grafo. Por ejemplo, supongamos este escenario en el que tenemos que alcanzar el punto B con el menor coste. Se puede pasar por las casillas en blanco mientras que las X representan muros:
| A | X | X | X | X | X | X | X | X | X | ||||||||||||||||||||
| X | X | X | X | X | X | X | X | X | |||||||||||||||||||||
| X | X | X | X | X | X | X | X | ||||||||||||||||||||||
| X | X | X | X | X | X | X | X | X | X | ||||||||||||||||||||
| X | X | X | B |
Una de las formas de elaborar este grafo podría ser simplemente numerar las casillas y crear una matriz de adyacencia. En esta matriz de adyacencia tendríamos desde qué nodo podemos ir a qué otro nodo. Para el caso del escenario anterior tendríamos que tenemos 5 filas por 30 columnas, son 150 casillas, es decir, 150 nodos.
| 0 | 5 | 10 | X | X | X | X | X | X | X | ||||||||||||||||||||
| 1 | 6 | 11 | X | X | X | X | X | X | X | X | |||||||||||||||||||
| 2 | 7 | 12 | X | X | X | X | X | X | X | ||||||||||||||||||||
| 3 | 8 | 13 | X | X | X | X | X | X | X | X | X | ||||||||||||||||||
| 4 | 9 | Etc | X | X | X | B |
Así de esta manera se podría ver que de la casilla 0 se puede saltar a la casilla 1, pero no a la 5 ni la 6 según el mapa anterior. Así de esta manera, esta matriz de adyacencia para la fila de la casilla 0 quedaría en todos ceros menos un 1 en la casilla 1. Entonces, desde la casilla 1 se puede volver a la 0, o ir a la 2. Así sucesivamente:
$casilla[0] = [0,1,0,0,0,0,0..0];
$casilla[1] = [1,0,1,0,0,0,0..0];
..En el siguiente apartado ya con código se puede ver más sencillo.
Generando grafos aleatoriamente en PHP

Recapitulando, la representación de muchos problemas se puede hacer mediante grafos. Así que el siguiente paso sería generar un sencillo script para generar grafos aleatorios. Eligiendo como sistema de representación una matriz de adyacencia podría quedar algo tal que así:
define('NUMBER_OF_NODES', 30);
$adjacentMatrix = [];
for ($from = 0; $from < NUMBER_OF_NODES; ++$from) {
for ($to = 0; $to < NUMBER_OF_NODES; ++$to) {
$adjacentMatrix[$from][$to] = 0 == rand(0, (int) NUMBER_OF_NODES / 10) ? rand(0, 9) : 0;
}
}Simplemente adjacentMatrix[i][j] representa el coste de ir del nodo i al j. Los valores se generan aleatoriamente, y no es muy denso el grafo, ya que no tiene muchos arcos, porque randomizando los valores sólo se rellenan algunos.
Los conjuntos, la lógica principal del algoritmo
La lógica principal se basa en llevar dos conjuntos de datos. Ya tenemos el grafo definido aleatoriamente, ahora toca ir del punto A al B. Para esto se va a llevar la información de dos conjuntos definidos como:
- Conjunto abierto.
- Conjunto cerrado.
El conjunto abierto será el que lleve los nodos que podemos expandir, usar para recorrer, que todavía no se hayan usado. La manera de ordenar, o de elegir el siguiente nodo, define variantes del algoritmo general.
De esta forma tendremos entonces que en el conjunto cerrado, almacenaremos los nodos encontrados, con su distancia o coste, nodos anteriores y posteriores posibles. Si un nodo no se ha recorrido, entonces se añadirá al conjunto abierto cuando se encuentre, si es que no es el nodo objetivo.
Y así sucesivamente se irán sacando nodos del conjunto abierto, mientras que se meten en el conjunto cerrado calculando sus valores y también en el conjunto abierto si son nuevos.
* Lo especial del algoritmo es que, si un nodo ya se ha alcanzado anteriormente por lo que ya está en el conjunto cerrado, hay que recalcular sus valores y los de los nodos relacionados, por si hemos llegado con un camino mejor que el que había almacenado.
Punto de partida
Partiendo de que para este codekata siempre partimos del nodo 0, entonces tenemos que inicializar los conjuntos:
$OPEN_SET = [0];
$CLOSED_SET = [
0 => [
'father' => null,
'children' => [],
'cost' => 0,
],
];La parte principal del algoritmo
Todo el núcleo del algoritmo quedaría con algo tal que así:
///////////////
// MAIN
// Searching in the graphs.
// Initially adding the starting node 0..
// The format for CLOSED is: node => [$father, [children], cost]
$OPEN_SET = [0];
$CLOSED_SET = [
0 => [
'father' => null,
'children' => [],
'cost' => 0,
],
];
// Get the goal node from the user input..
echo 'Start node is 0..'.PHP_EOL
.'Which will be the goal node to achieve (1 to '.(NUMBER_OF_NODES - 1).')? ';
$goalNode = readline();
// Start the main search..
$startTime = microtime(true);
echo 'Expanding nodes: ';
while (!empty($OPEN_SET)) {
$currentExpandingNode = array_shift($OPEN_SET);
echo $currentExpandingNode.'-';
if ($currentExpandingNode == $goalNode) {
returnTheWay($currentExpandingNode);
echo 'Time spent: '.(microtime(true) - $startTime).'secs.'.PHP_EOL;
exit;
}
$childrenNodes = getChildrenNodes($currentExpandingNode);
$CLOSED_SET[$currentExpandingNode]['children'] = $childrenNodes;
foreach ($childrenNodes as $childNode) {
if (isset($CLOSED_SET[$childNode])) {
// It's already in closed set..
fixClosedSet($childNode, $currentExpandingNode, $adjacentMatrix[$currentExpandingNode][$childNode]);
orderOpenSet();
} else {
// It's a new one..
$CLOSED_SET[$childNode] = [
'father' => $currentExpandingNode,
'children' => [],
'cost' => $CLOSED_SET[$currentExpandingNode]['cost']
+ $adjacentMatrix[$currentExpandingNode][$childNode],
];
mixOpenSet($childNode);
}
}
}
// END MAIN
///////////////////////Tiene añadido el preguntar al usuario por el nodo destino.
Funciones anexas al algoritmo
Una función que recorrería la matriz de adyacencia para pintarla por pantalla podría ser tal que así:
// Print adjacent matrix..
function printAdjacentMatrix()
{
global $adjacentMatrix;
echo 'ADJACENT MATRIX'.PHP_EOL;
echo ' | ';
for ($col = 0; $col < NUMBER_OF_NODES; ++$col) {
echo str_pad($col, 3, ' ');
}
echo PHP_EOL;
echo '------';
for ($col = 0; $col < NUMBER_OF_NODES; ++$col) {
echo '---';
}
echo PHP_EOL;
for ($from = 0; $from < NUMBER_OF_NODES; ++$from) {
echo str_pad($from, 3, ' ').'| ';
for ($to = 0; $to < NUMBER_OF_NODES; ++$to) {
echo str_pad($adjacentMatrix[$from][$to], 3, ' ');
}
echo PHP_EOL;
}
}Para sacar los nodos hijos, o lo que es lo mismo, los nodos adyacentes:
function getChildrenNodes($currentNode)
{
global $adjacentMatrix;
$childrenNodes = [];
for ($i = 0; $i < NUMBER_OF_NODES; ++$i) {
if ($i != $currentNode and $adjacentMatrix[$currentNode][$i] > 0) {
$childrenNodes[] = $i;
}
}
return $childrenNodes;
}Al añadir nuevos nodos al conjunto abierto, simplemente se añaden en el algoritmo general, con lo que simplemente se añaden al array del conjunto:
// Simply add node now..
function mixOpenSet($childNode)
{
global $OPEN_SET;
$OPEN_SET[] = $childNode;
}La citada anteriormente función de ordenación para el conjunto abierto. Aquí se establece el criterio de ordenación de los nodos siguientes que vamos a elegir para seguir el recorrido. Como se trata del algoritmo general simplemente no se ordenan. En el caso de derivaciones del algoritmo pueden ordenarse. Así que:
// Do nothing, not ordering..
function orderOpenSet()
{
}Estas siguientes dos funciones van juntas, porque se encargan de recalcular los costes de los caminos si llegamos a un nodo, por un arco nuevo, al que ya habíamos llegado antes. Si el nuevo camino tiene un coste menor, es decir, que es un mejor camino, entonces hay que recalcular los caminos:
// Recursive function to check and update costs and ways when necessary..
function fixClosedSet($childNode, $currentExpandingNode, $costToNewFromCurrent)
{
global $CLOSED_SET;
$currentCost = $CLOSED_SET[$childNode]['cost'];
$newCost = $CLOSED_SET[$currentExpandingNode]['cost'] + $costToNewFromCurrent;
if ($currentCost > $newCost) {
$CLOSED_SET[$childNode]['cost'] = $newCost;
$CLOSED_SET[$childNode]['father'] = $currentExpandingNode;
fixClosedSetList($childNode);
}
}
function fixClosedSetList($node)
{
global $CLOSED_SET, $adjacentMatrix;
foreach ($CLOSED_SET[$node]['children'] as $child) {
fixClosedSet($child, $node, $adjacentMatrix[$node][$child]);
}
}Y finalmente, la última función del codekata, que simplemente se usa cuando hemos alcanzado el nodo meta. De la forma en que si hemos llegado al nodo final, recorre hacia atrás el camino que hemos ido almacenando en el conjunto cerrado, que será el mejor camino de menor coste.
// Goes up node by node printing the way..
function returnTheWay($currentExpandingNode)
{
global $CLOSED_SET;
//var_dump($CLOSED_SET);
echo 'GOAL NODE FOUND!'.PHP_EOL;
$current = $currentExpandingNode;
$auxStr = $current.'('.$CLOSED_SET[$current]['cost'].')';
while (0 != $current) {
$current = $CLOSED_SET[$current]['father'];
$auxStr = $current.'('.$CLOSED_SET[$current]['cost'].') -> '.$auxStr;
//echo $auxStr.PHP_EOL;
//sleep(1);
}
echo $auxStr.PHP_EOL;
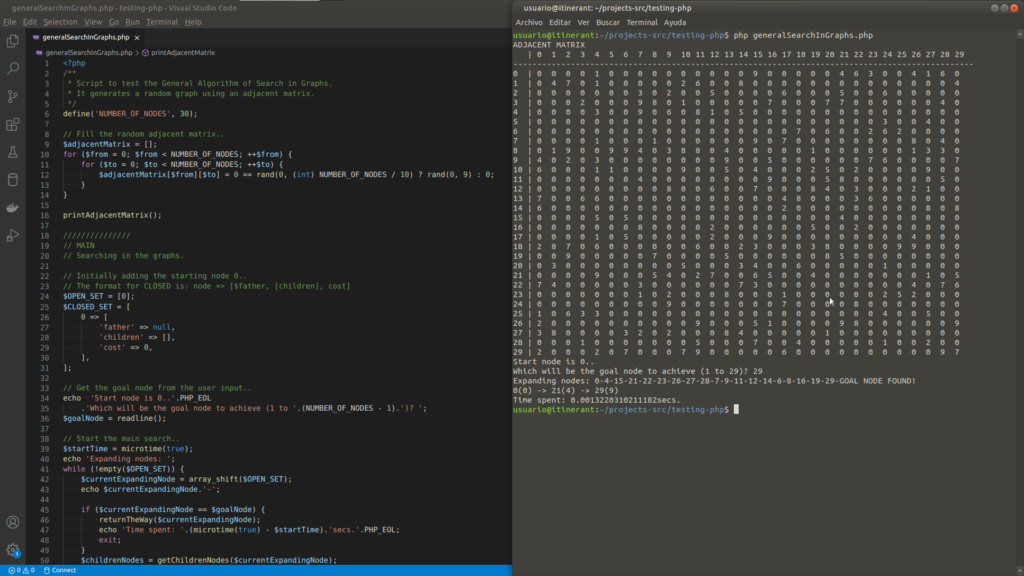
}Si el codekata ha ido bien, guardando todo en un fichero y ejecutándolo desde línea de comandos, se debería de ver algo como lo siguiente: