PrEDA: distribuir cosas no fraccionables en dos conjuntos equitativamente

Imaginemos que tenemos cosas de varios valores, y tenemos que dividir todo en dos partes. De forma que a cada parte le toca un conjunto de cosas de igual valor que a la otra parte.

Esto se da en casos como en la separación de bienes entre dos cónyuges, o cuando se liquida una sociedad entre dos socios, o en el reparto de un botín entre dos piratas o corsarios 😀 Con un poco más de desarrollo se puede generalizar para la división en N conjuntos.

Para atacar este problema la mejor estrategia de programación es la vuelta atrás. No es eficiente usar la fuerza bruta, tampoco podemos encontrar una forma de decidir la mejor partición para cada nuevo elemento para usar la estrategia voraz. Tampoco podemos usar el divide y vencerás. Y por último tenemos que encontrar no sólo una solución, sino todas las soluciones posibles. Así que no nos queda otra que recorrer creando un árbol de combinaciones. Pero sin entrar a comprobar todas las posibilidades ya que crearíamos un algoritmo de fuerza bruta. Sino que iremos sólo explorando el árbol de posibilidades que quizá nos sirven como solución. En cada ramificación pondremos cada nuevo objeto en un conjunto o en otro. Así que ramificaremos de dos en dos ya que vamos a divir en dos conjuntos. Viendo la salida por pantalla se verá claro..

Creando los datos para las pruebas

Comenzamos el script inicializando los objetos con sus valores, un vector de soluciones y unos contadores para sumar el valor de los objetos de cada partición. Sólo será posible usar el algoritmo si la suma de los valores de los objetos es par, ya que vamos a dividirlos en dos partes.

<?php

define('NUMBER_OF_THINGS', 4);
define('TRACE', false);
$thingsValues = array();
$solution = array();
$valuesSum = array(0, 0);
for ($i = 0; $i < NUMBER_OF_THINGS; ++$i) {
    $thingsValues[$i] = rand(1, 2); // value for each thing
    $solution[$i] = '#';
}
echo 'Value of '.NUMBER_OF_THINGS.' things: '.implode('-', $thingsValues).PHP_EOL;

Recorriendo el árbol de posibilidades volviendo atrás

Hay que notar que si un conjunto se pasa de la mitad del valor de los objetos ya no nos sirve esta solución. Cortaremos volviendo atrás en el árbol. Por otro lado, si llegamos a los nodos hojas de abajo del árbol llenando los dos conjuntos equitativamente, entonces tenemos una solución. Aquí el algoritmo:

startDistributeThingsWithDifferentValues($thingsValues, $solution, $valuesSum);

function startDistributeThingsWithDifferentValues($thingsValues, $solution, $valuesSum)
{
    $totalValuesSum = 0;
    foreach ($thingsValues as $key => $value) {
        $totalValuesSum += $value;
    }
    if ($totalValuesSum % 2 == 0) {
        distributeThingsWithDifferentValues($thingsValues, $solution, $valuesSum, $totalValuesSum, 0);
    } else {
        echo 'We can not divide things in equal parts!'.PHP_EOL;
    }
}

function distributeThingsWithDifferentValues($thingsValues, $solution, $valuesSum, $totalValuesSum, $k)
{
    if (isSolution($k, $valuesSum, $solution)) {
        echo ' ==>> SOLUTION FOUND! This one: '.implode('-', $solution).PHP_EOL;
    } else {
        for ($i = 0; $i < 2; ++$i) {
            $solution[$k] = $i;
            $valuesSum[$i] += $thingsValues[$k];

            if (TRACE) {
                echo 'Searching with $k='.$k
                    .', $solution='.implode('-', $solution)
                    .', $valuesSum='.implode('-', $valuesSum)
                    .', $totalValuesSum='.$totalValuesSum
                    .PHP_EOL;
            }

            if ($valuesSum[$i] <= $totalValuesSum / 2) {
                //echo ' Yet in allowed values.. $valuesSum='.implode('-', $valuesSum).PHP_EOL;
                if ($k < NUMBER_OF_THINGS) {
                    //echo ' going down..'.PHP_EOL;
                    distributeThingsWithDifferentValues($thingsValues, $solution, $valuesSum, $totalValuesSum, $k + 1);
                }
            }

            $valuesSum[$i] -= $thingsValues[$k];
        }
    }
}

function isSolution($k, $valuesSum, $solution)
{
    if (TRACE) {
        echo ' checking solution.. $k='.$k.', $valuesSum='.implode('-', $valuesSum).', $solution='.implode('-', $solution).PHP_EOL;
    }
    if ($k == NUMBER_OF_THINGS and $valuesSum[0] == $valuesSum[1]) {
        return true;
    } else {
        return false;
    }
}

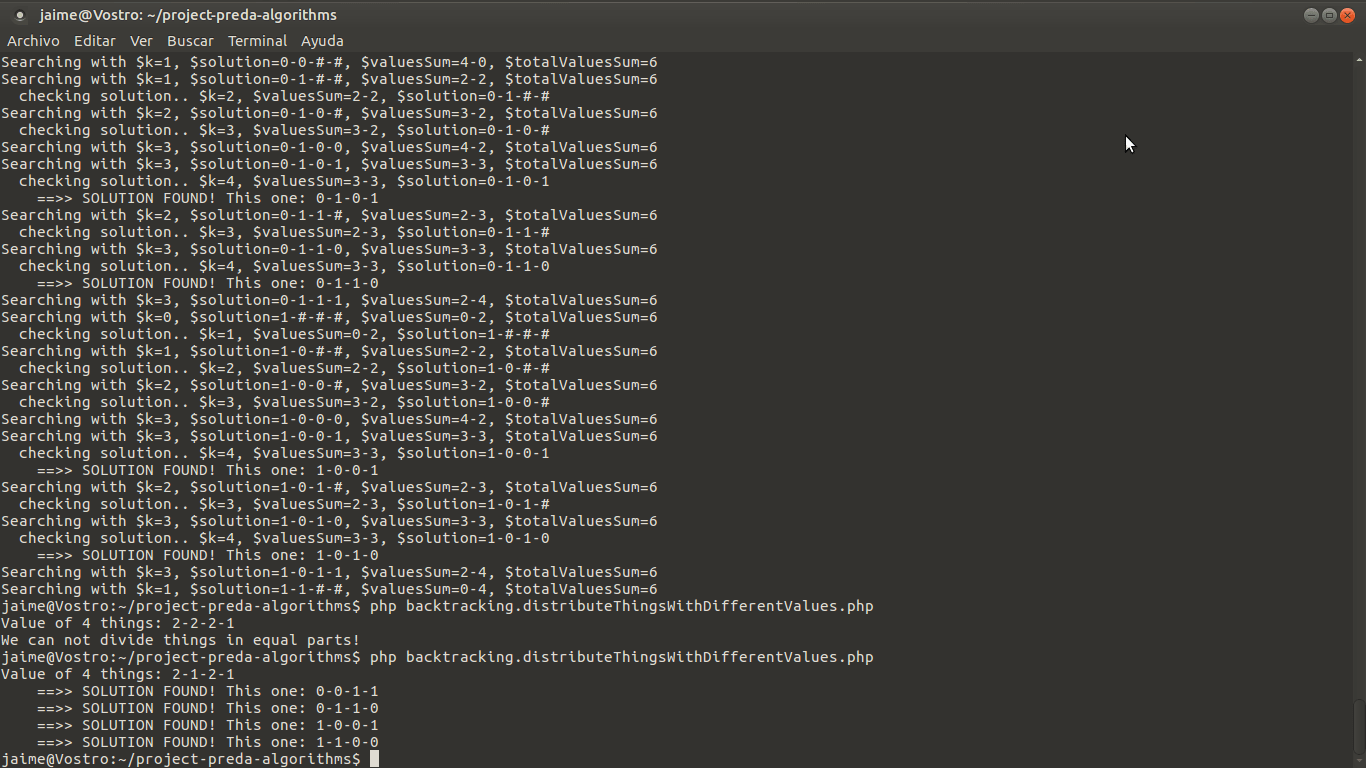
Mira que $k lleva la cuenta del nivel del árbol que llevamos. Se usa para ir trabajando cada objeto. El $valuesSum lleva la cuenta de los valores de los dos conjuntos. Fíjate cómo el vector $solución va poniendo los objetos en el conjunto 0 o en el 1, una # indica que ese objeto todavía no se ha repartido. Esto lo puedes poner en un PHP, y si todo va bien tienes que ver algo parecido a esto: